[알고리즘] 정렬 알고리즘

💡 tl;dr

---

• 버블 정렬 (Bubble Sort)
• 선택 정렬 (Selection Sort)
• 삽입 정렬 (Insertion Sort)
• 그외 정렬 알고리즘들

버블정렬 (Bubble Sort)

---

동작원리

• 배열의 0번부터 N-1번까지 탐색을 하면서 인접한 칸과 비교하여 swap 하는 방식

• Bubble 정렬을 오름차순으로 1회 실시하고 나서의 결과
• j번째 값과 j+1번째 값을 비교해서 만약 j번째의 값이 더 크다면 swap 해주는 식으로 동작
• 위의 과정을 첫번째는 0 ~ N-1번까지, 두 번째는 0 ~ N-2번까지, 세 번째는 0 ~ N-3번까지 … 식으로 진행되는데 이유는 위의 과정을 보면 알겠지만, 1회 실시하고 나게 되면 최댓값이 가장 마지막으로 가게 된다는 것을 알 수 있다.
• 즉, 2번째 과정에서는 이미 최댓값 위치에 저장되어있는 가장 마지막 값을 건드릴 필요가 없다.

시간복잡도

• 처음에는 N-1번탐색, 두 번째는 N-2번 탐색, … 이런식으로 진행되므로
  총 N-1 + N-2 + N-3 + N-4 + ... + 1 번 진행 = $\cfrac{N(N-1)}2$

• 식의 유도

  • 1, 2, 3, 4, 5 가 존재할 때, 1회 탐색할때 총 1부터 5까지 4번 탐색을 하게된다.
  • 2회 탐색할 때에는 1부터 4까지 3번탐색, 3회는 2번, 4회는 1번 … 총 4 + 3 + 2 + 1 = 10회 탐색을 하게된다.
  • 이 10을 식을 이용해서 도출해 내면 (5 x 4) / 2로 표현할 수 있게 된다. 따라서 위의 식 만큼의 탐색을 하게 된다.
  • 따라서 $\cfrac12N^2 - \cfrac12N$ 이라는 시간복잡도를 갖게 되고, $O(N^2)$ 으로 표기할 수 있다.

• worst case

  • 역방향으로 정렬이 되어 있는 경우
  • $O(N^2)$
• best case
  • 이미 정렬이 되어 있는 경우
  • $O(N^2)$
• 즉, Bubble정렬의 경우 최악이든 최선이든 똑같이 $O(N^2)$만큼의 시간복잡도를 갖게 된다.

선택 정렬 (Selection Sort)

---

동작 원리

• 가장 먼저 제일 앞에 값을 ‘최소값을 가진 Index’ 라고 가정을 하고 탐색 시작.
• 탐색 진행 중, 만약 ‘최소값을 가진 Index’보다 더 작은 값을 가진 값이 나오면, ‘최소값을 가진 Index’를 더 작은 값을가진 Index번호로 변경. 이 과정을 N-1번까지 진행.
• 이후에, 제일 앞 Index 번호와, 최소값을 가진 Index번호가 다르다면 swap 해주면 되는 방식

• 위 그림은 1회전 시켰을 때의 결과값이다.
• 그렇다면 2회전 시킬 때 시작점을 어디로 잡으면될까?
  • 1번으로 시작하면 된다.
  • 왜냐하면 0번에는 이미 최소값이 자기 자리를 찾아서 정렬되어 있기 때문에 더 이상 관리할 필요가 없기 때문이다.

// 선택정렬 함수
void Selection_Sort(){
  // 0부터 끝까지 전체탐색
  for(int i = 0 ; i < MAX; i++){
    // 가장 작은 값이 저장된 Index를 탐색을 시작하는 Index로 가정하고 탐색시작.
    int Min_Index = i;
  
    // i + 1번부터 끝까지 탐색을 하는데
    for(int j = i  + 1; i j < MAX; j++){

        // 만약 더 작은 값이 나오면 Min_Index값 변경
        if(Arr[j] < Arr[Min_Index]) Min_Index = j;
    }

    // 만약 변화가 있었다면 swap.
    if(i != Min_Index) swap(Arr[i], Arr[Min_Index]);
  }
}

시간 복잡도

• 선택정렬의 경우, 가장 처음에 총 N-1번의 탐색을 하게 된다.
• 2회전 때는 정렬된 가장 첫번째 값(최소값)을 빼고 N-2번 탐색을 하게된다.
• 즉, 끝까지 탐색을 하게되면 결과적으로 N-1 + N-2 + N-3 + ... + 1 번 탐색.
• 이를 수식으로 나타내면 $\cfrac12N^2 - \cfrac12N$ 번 탐색을 하게되고, $O(N^2)$이 된다.
• worst case
  • 역방향으로 정렬되어 있는 경우
  • N-1 + N-2 + N-3 + ... + 1번 탐색
  • $O(N^2)$
• best case
  • 이미 정렬이 되어 있는 경우
  • $O(N^2)$

삽입 정렬 (Insertion Sort)

---

동작 원리

• 삽입정렬은 앞으로 가면서 탐색을 진행한다.
• N만큼의 크기의 배열을 선언하고 0부터 N-1 번까지의 배열을 사용할때, Index 1번부터 탐색을 진행한다.
• 왜냐하면 앞으로 가면서 탐색을 하는 방식이기 때문에 0번 Index는 의미가 없기 때문

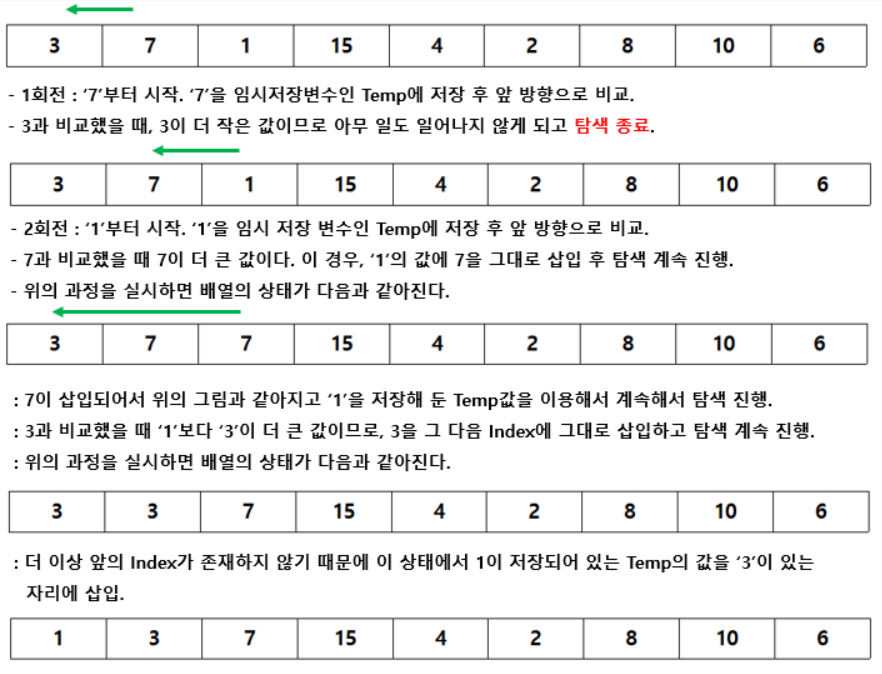
• 앞부분에 대해서만 정렬하는 과정
• 시작 Index를 기점으로 앞으로 쭉 탐색을 진행하는데, 2가지 조건이 있다.
  1. Index가 0보다 크거나 같을때
     • 0보다 작은 Index는 존재하지 않기 때문에 아무리 탐색을 많이 하더라도 0보다 크거나 같을 때 까지만 탐색이 가능하다.
  2. 비교하는 값이 더 클때
     • 앞의 값이 더 크다면 특정한 과정을 진행한 후 탐색을 계속하지만, 값이 더 작으면 앞쪽 배열은 이미 정렬이 완료된 상태 그대로 탐색을 종료한다.
• 특별한 과정
  • 현재 값을 Temp 에 저장하고, 비교 값(Temp보다 작은 값)을 현재 index에 복사.
  • 만약 비교값이 같거나 크다면 해당 비교 index에 Temp값 삽입
  • 비교값의 index가 0보다 작아지기 전까지 위 과정 반복

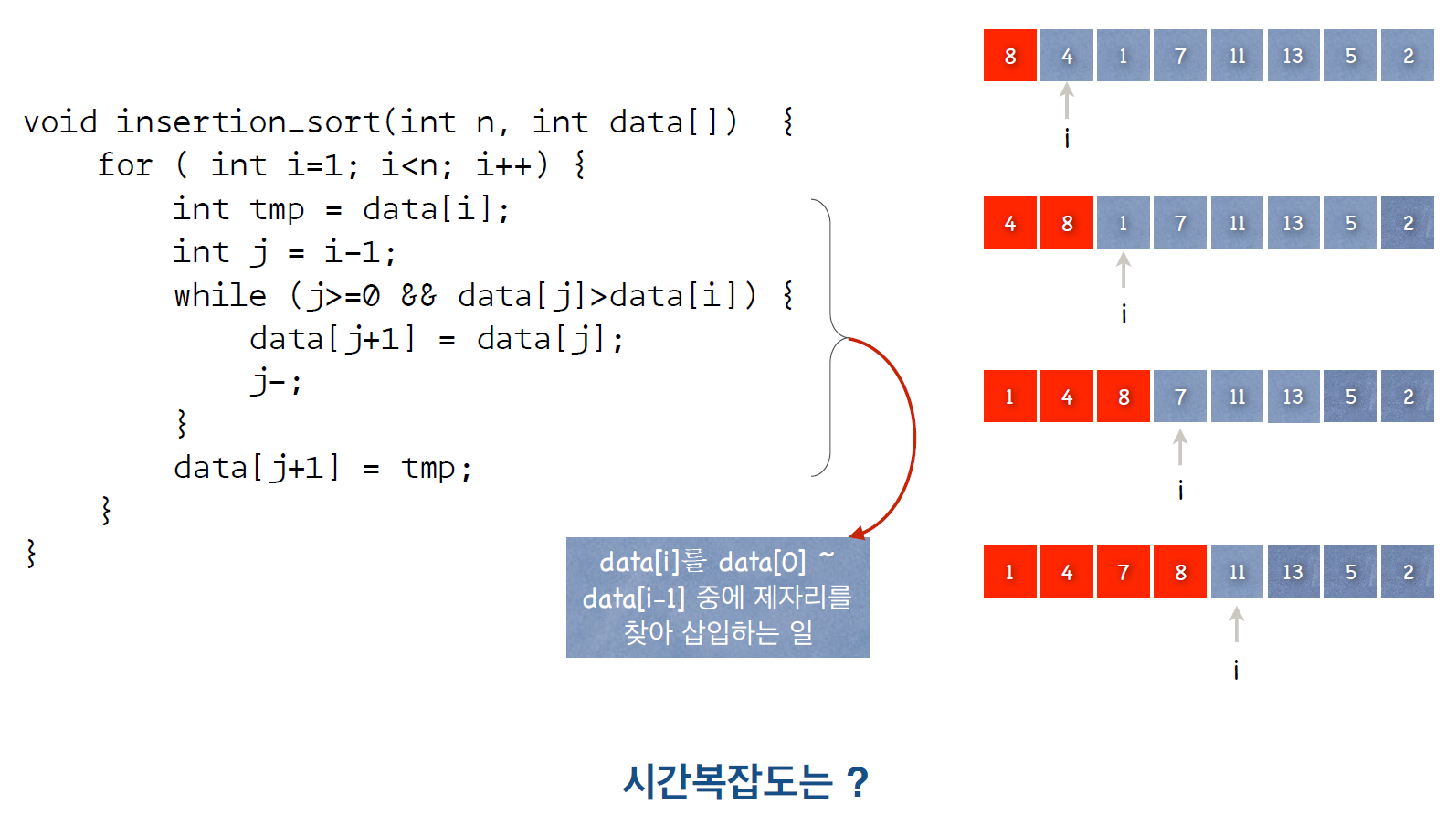
void Insertion_Sort(){
  // 1번 Index부터 마지막 Index까지 탐색. 0번 Index는 탐색 X
  for(int Cur_Index = 1; Cur_Index < MAX; Cur_Index++){
    // 현재의 값을 Temp라는 임시 저장 변수에 저장.
    int Temp = Arr[Cur_Index];
    // Index를 관리하는 변수. 현재 Index - 1번부터 탐색 시작.
    int Before_Index = Cur_Index -1;	
    // Index번호가 0보다 크거나 같고, 이전 값이 더 큰 경우만
    
    while( Before_Index >= 0 && Arr[Before_Index] > Temp {
      // 값을 그대로 복사해서 넣어주고
      Arr[Before_Index + 1] = Arr[Befored_Index];
      // 탐색 계속해서 진행
      Before_Index = Before_Index - 1;
    }
    
    // 탐색이 종료되면, 올바른 배열을 만들어 주기 위해서 값 삽입.
    Arr[Before_Index + 1] = Temp;
  }
}

시간 복잡도

• 삽입정렬은 최악의 경우와 최선의 경우 시간의 차이가 많이 정렬법이다.
• worst case
  • 역정렬 되어있는 경우
  • $\cfrac{N(N-1)}2$ 번 시행
  • $O(N^2)$
• best case
  • 이미 정렬이 되어있는 경우
  • 모든 현재값이 비교값보다 같거나 크므로 1번씩 x N 번 시행
  • $O(N^2)$

다른 정렬 알고리즘

---

퀵소트(quick sort) 알고리즘

• 최악의 경우 $O(N^2)$, 하지만 평균 시간복잡도는 $O(Nlog_2{N})$

합병정렬(merge sort)

최악의 경우 $O(Nlog_2{N})$

힙 정렬(heap sort)

최악의 경우 $O(Nlog_2{N})$

참고

---

영리한 프로그래밍을 위한 알고리즘 강좌 (권오흠) - 인프런