[알고리즘] 시간복잡도와 점근적 표기법

💡 tl;dr

---

• 시간복잡도
• 점근적 표기법
• 복잡도 비교

시간복잡도

---

• 실행시간의 분석 : 실행시간은 실행환경에 따라 달라짐
  • 하드웨어, 운영체제, 언어, 컴파일러 등
• 실행 시간을 측정하는 대신 연산의 실행 횟수를 카운트
• 연산의 실행 횟수는 입력 데이터의 크기에 관한 함수로 표현
• 데이터의 크기가 같더라도 실제 데이터에 따라서 달라짐
  • 최악의 경우 시간복잡도 (worst-case analysis)
  • 평균 시간복잡도 (average-case analysis)

점근적 표기법

---

• 점근적 표기법을 사용
  • 데이터의 개수 n→∞일때 수행시간이 증가하는 growth rate로 시간복잡도를 표현
    하는 기법
  • Θ-표기, Ο-표기 등을 사용
• 유일한 분석법도 아니고 가장 좋은 분석법도 아님
  • 다만(상대적으로) 가장 간단하며
  • 알고리즘의 실행환경에 비의존적임
  • 그래서 가장 광범위하게 사용됨
• 알고리즘에 포함된 연산들의 실행 횟수를 표기하는 하나의 기법
• 최고차항의 차수만으로 표시
• 따라서 가장 자주 실행되는 연산 혹은 문장의 실행횟수를 고려하는 것으로 충분

점근표기법: Ο-표기

---

점근표기법: Ω-표기

---

점근표기법:Θ-표기

---

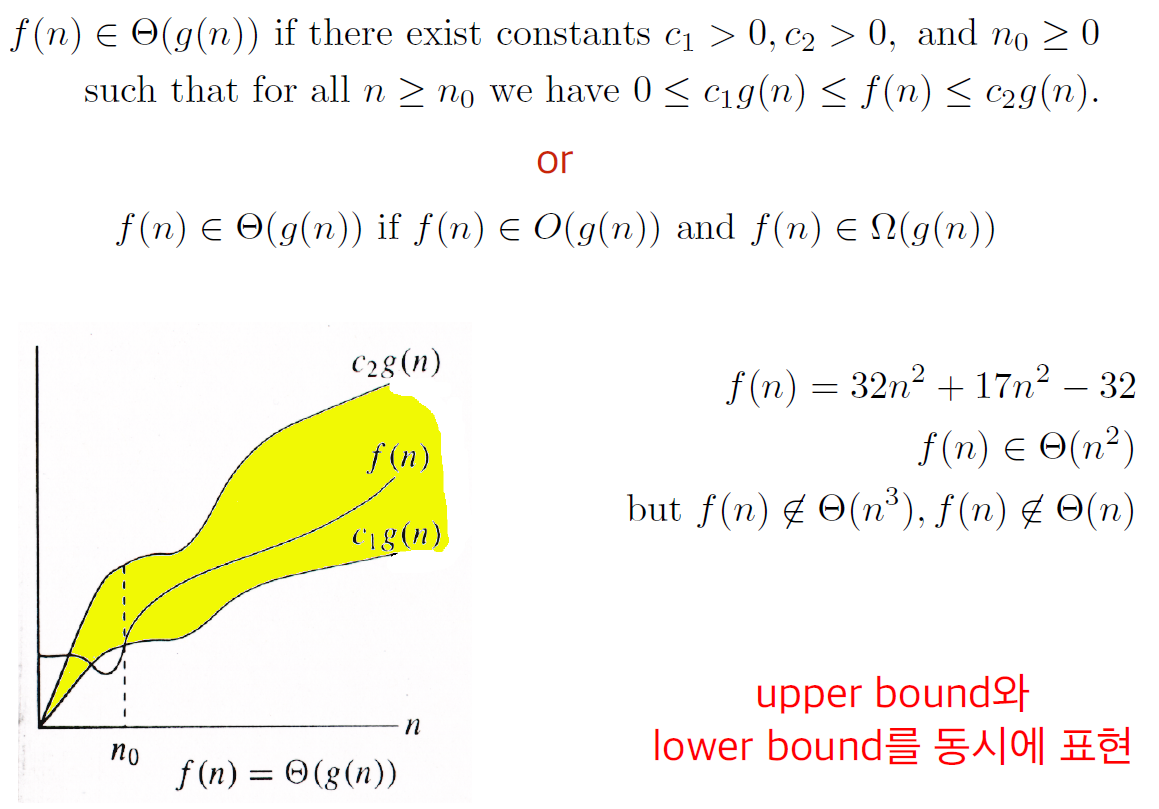
• f(n) ∈ O(g(n))을 f(n) = O(g(n))으로 쓰는 경우가 많음
• 차수가 k≥0인 모든 다항식은 O(nᵏ)이다.

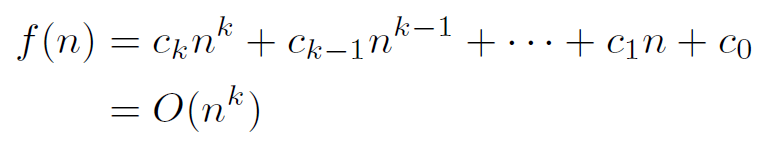
차수가 p인 다항식과 q인 다항식의 합

---

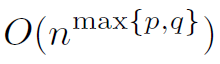
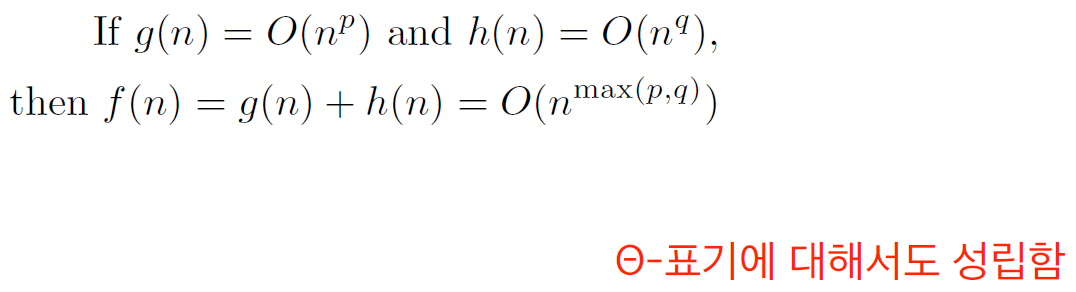
복잡도 비교

---

• 알고리즘은 실행 시간이 다항식 인 경우 효율적

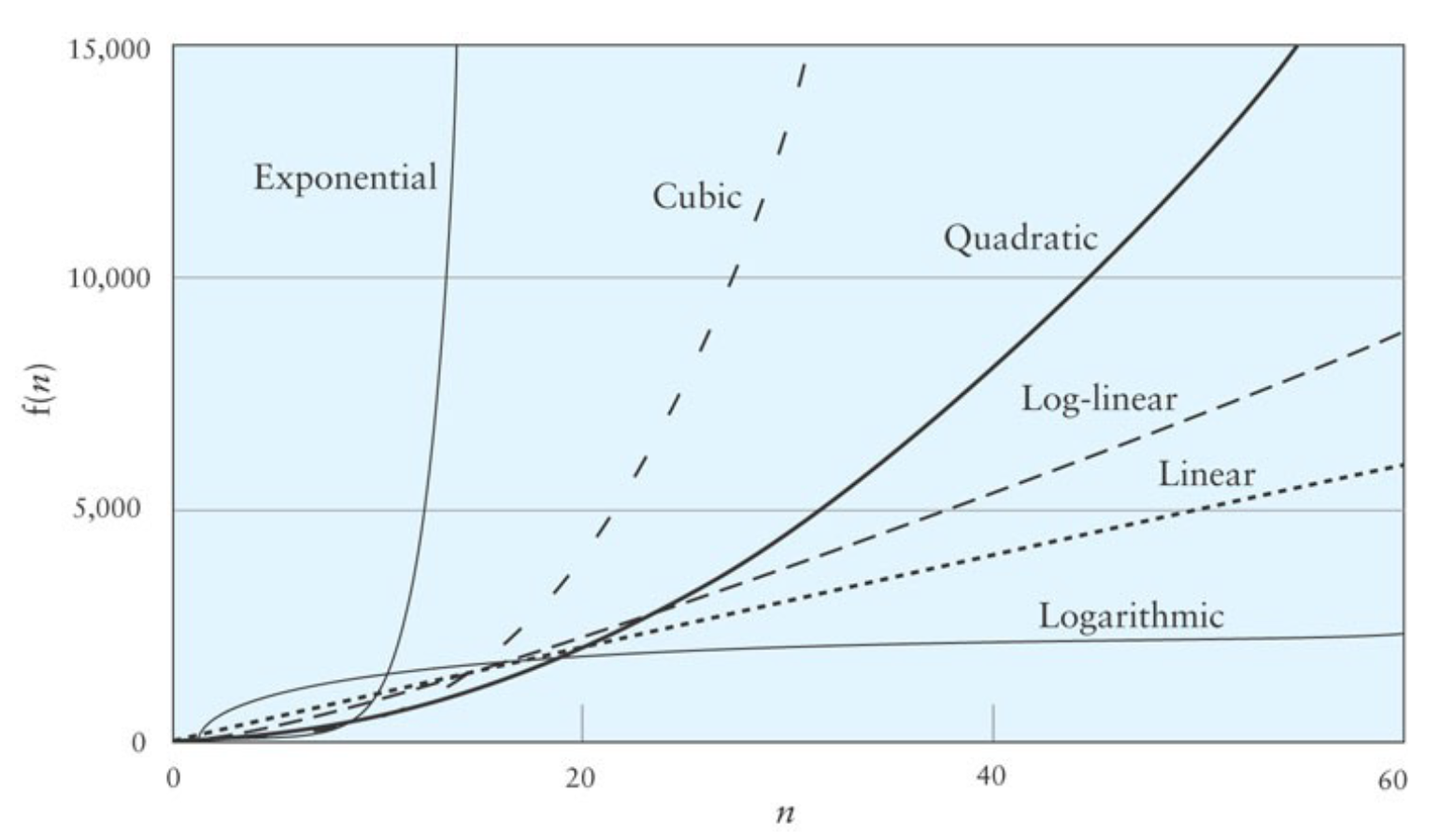
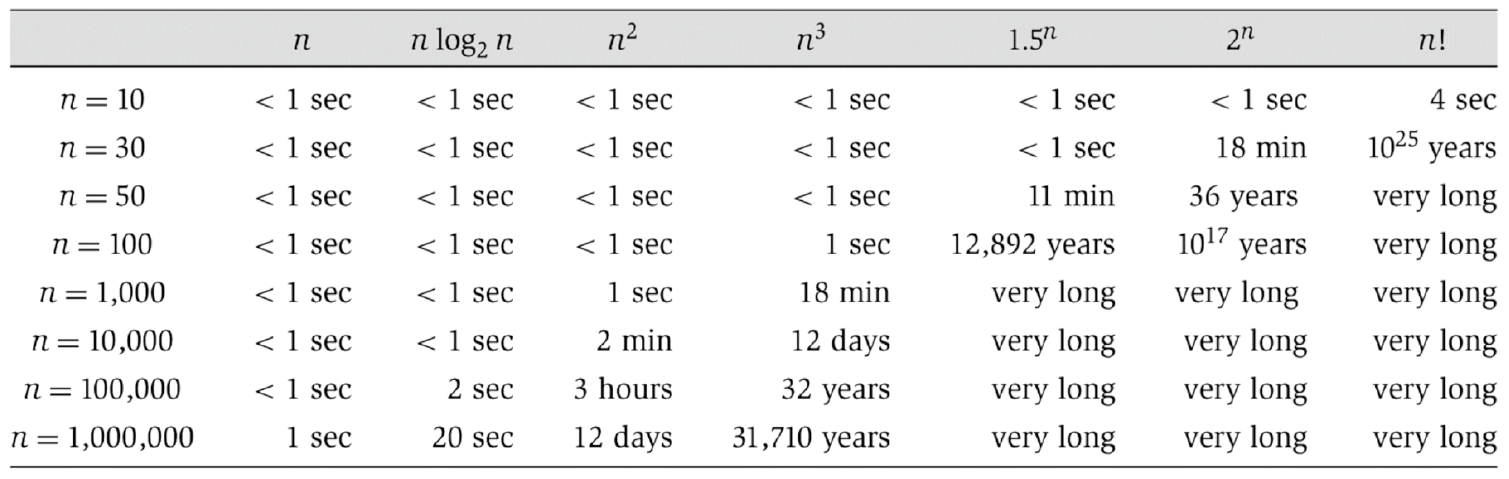
참고

---

영리한 프로그래밍을 위한 알고리즘 강좌 (권오흠) - 인프런