2021, 7월 28일, 수요일 오후 9:45알고리즘 / 개념14분안에 읽기 (약 2052 단어)0회 방문

[알고리즘] 서로소 집합 자료 구조 (Disjoint Set)

💡 tl;dr

서로소 집합 자료구조(Disjoint set)
서로소 집합 연결 리스트 (Disjoint-set linked lists)
서로소 집합 숲 (Disjoint-set forest)
최적화

서로소 집합 자료 구조 (Disjoint Set)

서로소 집합 자료 구조란 서로소 부분 집합으로 나눠진 원소들에 대한 정보를 다루는 자료구조다.

여기서 서로소 집합은 공통 원소가 없는 두 집합을 뜻한다.

즉, 서로소 집합 자료구조는 상호 배타적인 부분 집합들로 이루어진 원소들을 다루는 자료구조다.

서로소 집합(disjoint-set) 자료 구조
합집합-찾기(union-find) 자료 구조
병합-찾기 집합(merge-find set)

위 3가지 자료 구조는 모두 서로소 부분 집합을 다룬다.

사용 함수

파인드(Find): 어떤 원소가 주어졌을 때 이 원소가 속한 집합을 반환한다. 일반적으로 같은 집합인지 판단하기 위해 집합을 대표하는 원소를 반환한다.
유니온(Union): 두 개의 집합을 하나의 집합으로 합친다.
메이크셋(MakeSet): 특정 한 원소만을 가지는 집합을 만든다.

이 세 가지 연산을 활용하여 많은 파티션(partitioning) 문제들을 해결 할 수 있다.

서로소 집합 연결 리스트 (Disjoint-set linked lists)

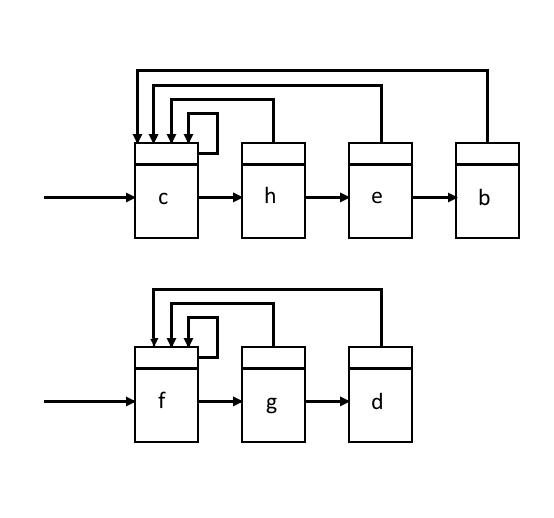
각 노드가 head를 가르키는 서로소 집합 연결 리스트

서로소 집합 데이터 구조는 간단히 집합을 표현하기 위해 연결 리스트(linked list)를 사용한다.
각 리스트의 헤드(head) 부분에는 해당 집합의 대표 원소를 저장한다.
MakeSet은 한 원소만을 가지는 리스트를 생성한다.
Union은 두 리스트를 붙이는 연산을 수행한다. 이때 한 리스트의 헤드 부분이 다른 리스트의 꼬리를 가리켜 상수 시간(constant-time) 연산을 수행한다.
Find 수행시 특정 원소로부터 리스트의 헤드까지 반대 방향으로 탐색해야 하므로 이 소요된다.
- 이 단점은 각 연결 리스트 노드에 헤드를 가리키는 포인터를 포함시켜 해결 할 수 있다. 이 때문에 상수 시간으로 대표 원소를 바로 참조할 수 있다.
- 그러나 이 경우 Union 연산시 head를 갱신해야하므로 $O(n)$ 이 요구된다.

가중치-유니온 휴리스틱 (weighted-union heuristic)

서로소 집합 연결 리스트(Disjoint-set linked lists)의 성능 향상 방법.
만약 각 리스트의 길이를 추적(길이 기준 sorting 등)할 수 있다면, 항상 짧은 리스트를 긴 리스트에 덧붙이며 요구 시간(required time) 성능을 향상시킬 수 있다.
n개의 원소들의 m개의 연이은 MakeSet, Union, Find를 수행할 경우 $O(m + nlogn)$ 시간을 요구한다.
점근적으로(asymptotically) 더 빠른 연산을 위해서 다른 자료 구조(Tree 등)가 필요하다.

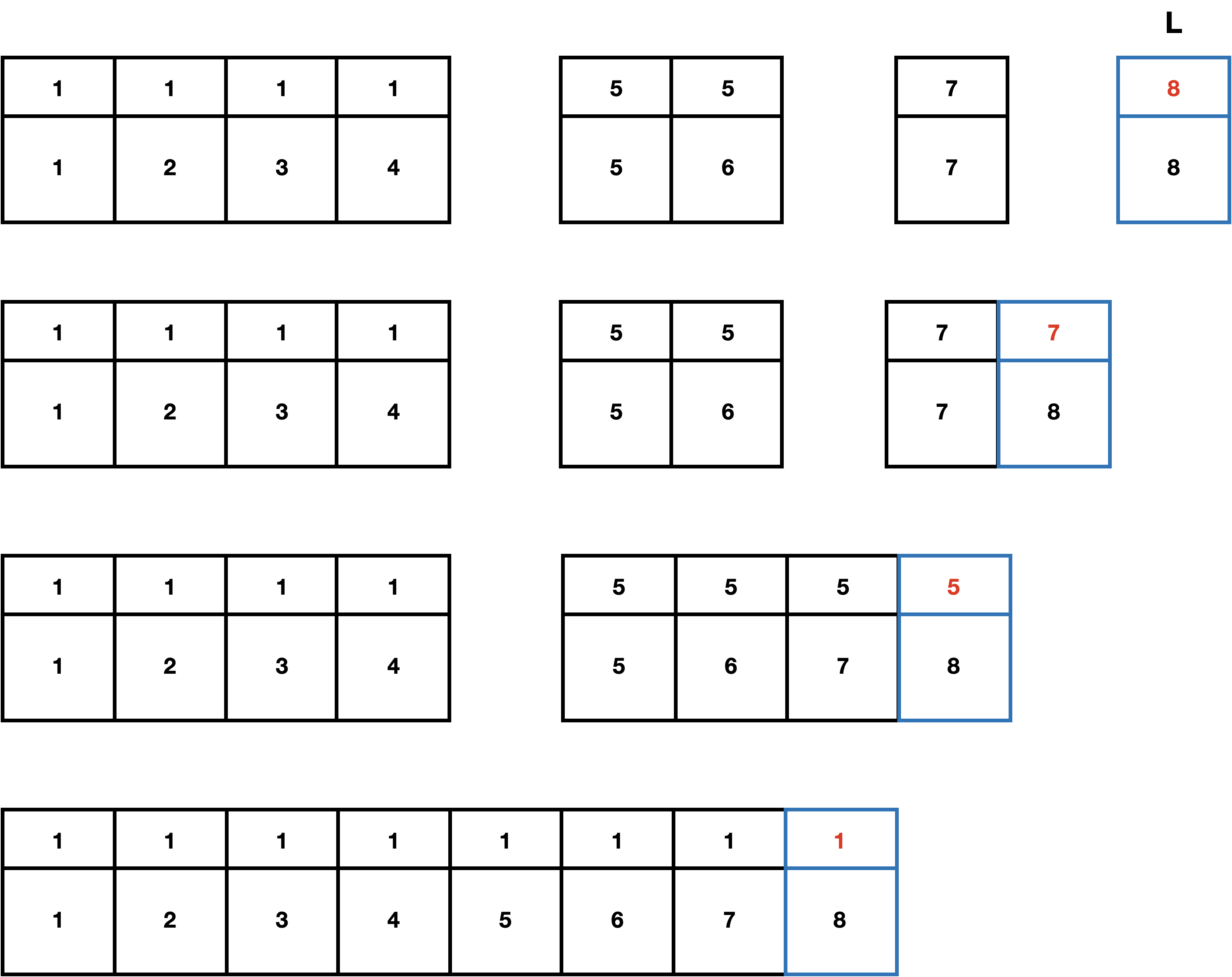
리스트 L 원소의 병합과정 비용

위 그림에서 전체 노드의 갯수는 n(n=8)이고 연결 리스트 L은 1개의 원소를 담은 배열이다. 배열 L이 자신보다 길이가 같거나 큰 배열과 Union을 수행한다면 매 수행마다 길이가 2배가 되야 한다. 이때 발생하는 비용은 정확히 $log_{2}{n}$ 이다.

따라서 특정 리스트(L)안의 특정 원소(node 8)는 최악의 경우 $log_{2}{n}$ 번의 갱신이 필요하다. 그러므로 n개의 원소를 가지는 한 리스트는 최악의 경우 $O(nlog{n})$ 의 시간이 걸린다. 이 구조에서 각 노드는 원소가 속한 리스트의 이름(head)을 포함하므로 Find 연산은 $O(1)$ 의 시간이 걸린다.

서로소 집합 숲 (Disjoint-set forest)

서로소 연결 리스트에 트리(Tree)를 접목한 자료구조
각 노드들은 부모 노드를 참조
각 집합의 대표는 해당 트리의 루트(root) 노드
Find는 루트 노드에 도달할 때까지 부모 노드를 따라 참조
Union은 한 루트 노드를 다룬 루트 노드에 연결하여 병합
최악의 경우 매우 불균형한 트리를 생성하여 연결 리스트와 동일

함수 (Python)

# makeSet
parent = [0] * (N+1) # 부모 테이블 초기화

# 부모 테이블 상에서 자기 자신을 부모로 설정
for i in range(1, N+1):
    parent[i] = i
    
def find(a): # a 정점의 루트 노드 탐색
    if parent[a] == a: # a가 루트 노드이면, a 반환
        return a
    return find(parent[a]) # 루트가 아니면 a의 부모 노드로 재탐색
  
def union(a, b): # a와 b 집합을 병합
    a = find(a) # a의 루트 노드 탐색
    b = find(b) # b의 루트 노드 탐색
    parent[a] = parent[b]

최악의 경우

최악의 경우 연결 리스트와 동일한 효율성을 갖는다.
아래 두 가지 방법을 통해 성능을 개선할 수 있다.

유니온 바이 랭크(Union by rank)

유니온 바이 랭크

항상 작은 트리를 큰 트리 루트에 붙이는 방법
두 트리의 깊이가 같을 경우에만 깊이가 증가
만약 경로 압축을 활용하면 깊이가 같을 경우 알고리즘 동작이 멈추므로 깊이 대신 rank란 용어 사용
한 개의 원소를 가지는 트리의 랭크 = 0
같은 랭크 r을 가지는 두 트리가 합쳐질 경우 r+1의 트리가 만들어짐
이때 Union 또는 Find 연산은 $O(logn)$ 을 가진다.

[향상된 MakeSet]

1
2
3

# makeSet
parent = [0] * (N+1) # 부모 테이블 초기화
rank = [0] * (N+1) # 정점의 rank를 저장

[향상된 Union]

def union(a, b): # a와 b 집합을 병합
    a = find(a) # a의 루트 노드 탐색
    b = find(b) # b의 루트 노드 탐색
    if a == b: # 루트 노드가 동일하면, 동일한 집합
        return
    if rank[a] > rank[b]: # rank가 낮은 집합을 rank가 높은 집합으로 병합
        parent[b] = a # 병합
    else:
        parent[a] = b # 집합 병합
        if rank[a] == rank[b]: # 두 랭크가 동일하면
            rank[b] += 1 # 랭크 +1

경로 압축 (path compression)

경로 압축

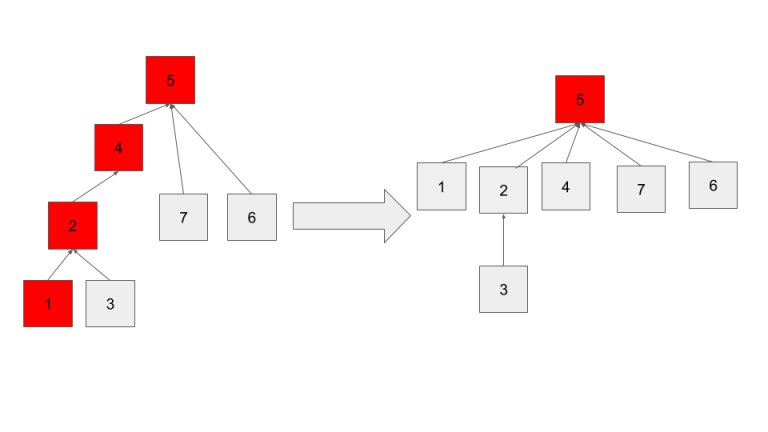
파인드 연산을 수행 할 때마다 트리의 구조를 평평하게 만드는 방법
방문한 각 노드들이 직접 루트 노드를 가리키도록 갱신하는 것
모든 노드가 같은 대표 노드를 공유
최종 생성된 트리는 보다 평평해짐
해당 원소뿐만 아니라 직/간접적으로 참조하는 연산들의 속도를 빠르게 해줌
Find 연산이 시간 복잡도를 좌우하며 $O(N-1)$ 을 따른다.

[향상된 Find]

def find(a): # a 정점의 루트 노드 탐색
    if parent[a] == a: # a가 루트 노드이면, a 반환
        return a
    p = find(parent[a]) # 루트 노드 탐색
    parent[a] = p # a의 루트 노드 갱신
    return parent[a]

최적화

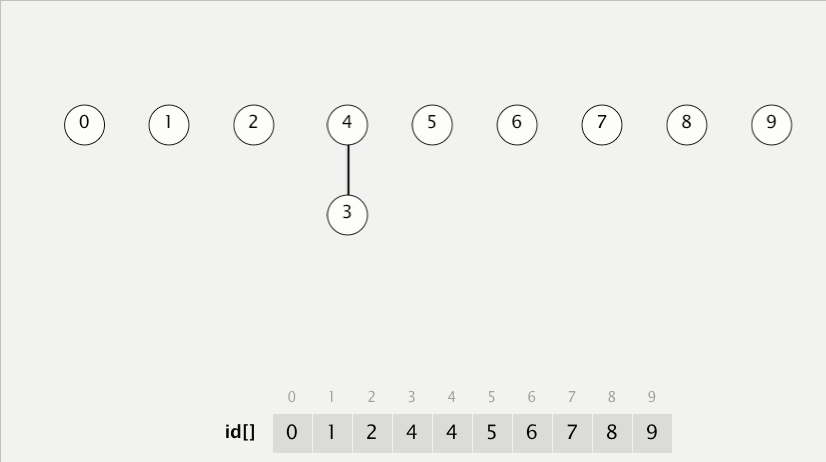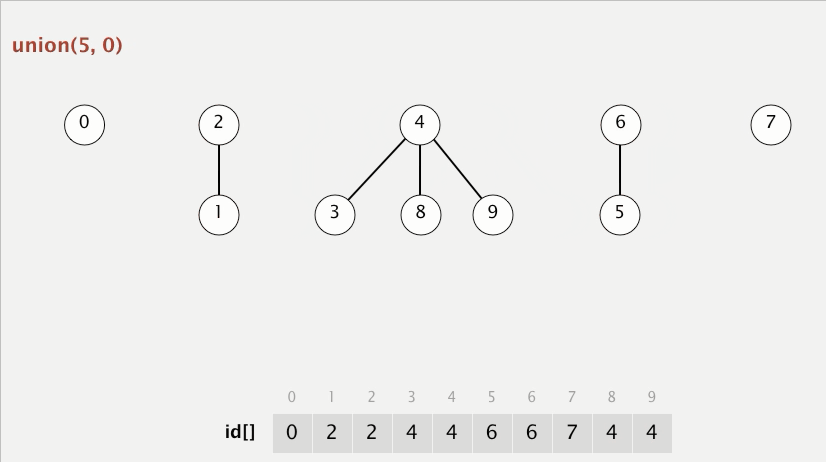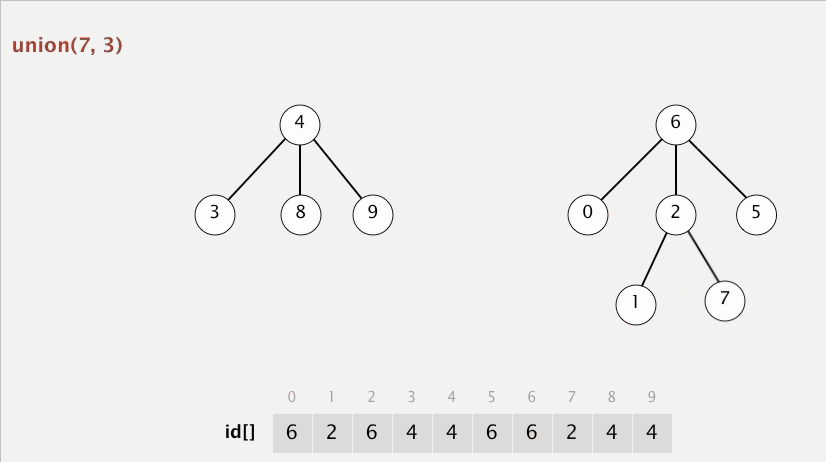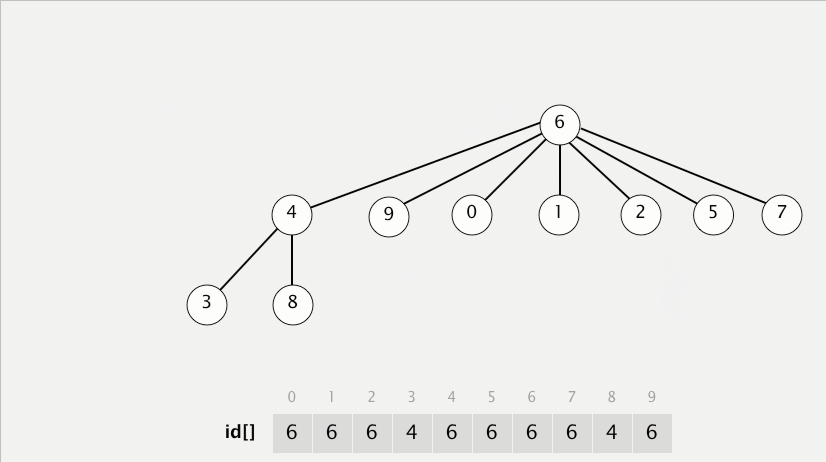
유니온 바이 랭크 + 경로 압축

[최적화 코드 - python]

N = int(input()) # 노드 수 입력 받기
M = int(input()) # 정점 수 입력 받기
parent = [0] * (N+1) # 부모 테이블 초기화
rank = [0] * (N+1) # 정점의 rank를 저장

# 부모 테이블 상에서 자기 자신을 부모로 설정
for i in range(1, N+1):
    parent[i] = i
    
# union find algorithm
def find(a): # a 정점의 루트 노드 탐색
    if parent[a] == a: # a가 루트 노드이면, a 반환
        return a
    p = find(parent[a]) # 루트 노드 탐색
    parent[a] = p # a의 루트 노드 갱신
    return parent[a]

def union(a, b): # a와 b 집합을 병합
    a = find(a) # a의 루트 노드 탐색
    b = find(b) # b의 루트 노드 탐색
    if a == b: # 루트 노드가 동일하면, 동일한 집합
        return
    if rank[a] > rank[b]: # rank가 낮은 집합을 rank가 높은 집합으로 병합
        parent[b] = a # 병합
    else:
        parent[a] = b # 집합 병합
        if rank[a] == rank[b]: # 두 랭크가 동일하면
            rank[b] += 1 # 랭크 +1