[프로그래머스] (LV4) 미로 탈출

미로 탈출

Python3

문제 설명

신규 게임 ‘카카오 미로 탈출’이 출시되어, 라이언이 베타테스터로 참가했습니다.

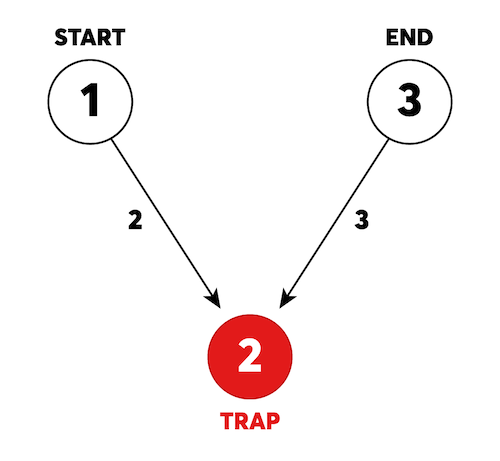
위 예시 그림은 카카오 미로 탈출의 초기 상태를 나타냅니다. 1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는데 걸리는 시간이 표시되어 있습니다. 길은 화살표가 가리키는 방향으로만 이동할 수 있습니다. 미로에는 함정이 존재하며, 함정으로 이동하면, 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.\
출발지점인 1번 방에서 탈출이 가능한 3번 방까지 이동해야 합니다. 탈출하는데 걸리는 최소 시간을 구하려고 합니다.

• 그림의 원은 방을 나타내며 원 안의 숫자는 방 번호를 나타냅니다.
  • 방이 n개일 때, 방 번호는 1부터 n까지 사용됩니다.
• 화살표에 표시된 숫자는 방과 방 사이를 이동할 때 걸리는 시간을 나타냅니다.
  • 화살표가 가리키고 있는 방향으로만 이동이 가능합니다. 즉, 위 그림에서 2번 방에서 1번 방으로는 이동할 수 없습니다.
• 그림에 표시된 빨간색 방인 2번 방은 함정입니다.
  • 함정 방으로 이동하는 순간, 이동한 함정 방과 연결되어있는 모든 길의 방향이 반대가 됩니다.
  • 위 그림 1번 방에서 2번 방으로 이동하는 순간 1에서 2로 이동할 수 있던 길은 2에서 1로 이동할 수 있는 길로 바뀌고, 3에서 2로 이동할 수 있던 길은 2에서 3으로 이동할 수 있는 길로 바뀝니다.
  • 똑같은 함정 방을 두 번째 방문하게 되면 원래 방향의 길로 돌아옵니다. 즉, 여러 번 방문하여 계속 길의 방향을 반대로 뒤집을 수 있습니다.
• 미로를 탈출하는데 필요한 최단 시간은 다음과 같습니다.
  • 1→2: 2번 방으로 이동합니다. 이동 시간은 2입니다.
  • 함정 발동: 2번 방과 연결된 모든 길의 방향이 반대가 됩니다.
  • 2→3: 3번 방으로 이동합니다. 이동 시간은 3입니다.
  • 탈출에 성공했습니다. 총 이동시간은 5입니다.

방의 개수를 나타내는 정수 n, 출발 방의 번호 start, 도착 방의 번호 end, 통로와 이동시간을 나타내는 2차원 정수 배열 roads, 함정 방의 번호를 담은 정수 배열 traps이 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최단 시간을 return 하도록 solution 함수를 완성해주세요.

---

제한사항

• 2 ≤ n ≤ 1,000
• 1 ≤ start ≤ n
• 1 ≤ end ≤ n
• 1 ≤ roads의 행 길이 ≤ 3,000
• roads의 행은 [P, Q, S]로 이루어져 있습니다.
  • P에서 Q로 갈 수 있는 길이 있으며, 길을 따라 이동하는데 S만큼 시간이 걸립니다.
  • 1 ≤ P ≤ n
  • 1 ≤ Q ≤ n
  • P ≠ Q
  • 1 ≤ S ≤ 3,000
  • 서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있습니다.
• 0 ≤ traps의 길이 ≤ 10
  • 1 ≤ traps의 원소 ≤ n
  • 시작 방과 도착 방은 함정이 아닙니다.
• 항상 미로를 탈출할 수 있는 경우만 주어집니다.

---

입출력 예

n	start	end	roads	traps	result
3	1	3	[[1, 2, 2], [3, 2, 3]]	[2]	5
4	1	4	[[1, 2, 1], [3, 2, 1], [2, 4, 1]]	[2, 3]	4

---

입출력 예 설명

입출력 예 #1

문제 예시와 같습니다.

입출력 예 #2

1 → 2 → 3 → 2 → 4 순서로 이동하면 됩니다. 총 이동시간은 4입니다.

---

제한시간 안내

• 정확성 테스트 : 10초

풀이

---

python

import heapq as h
def solution(n, start, end, roads, traps):
    start -=1; end -=1;
    INF = float("inf");
    graph = [[] for _ in range(n)]
    trap_dict = {trap-1:idx for idx, trap in enumerate(traps)};
    nodes = [];
    isVisit = [[False]*n for _ in range(1<<len(traps))]
    
    for road in roads:
        start_i, end_i, cost = road
        graph[start_i-1].append([end_i-1,cost,0])
        graph[end_i-1].append([start_i-1,cost,1])
    
    h.heappush(nodes,(0,start,0))
    while nodes:
        cur_time, cur_node, state = h.heappop(nodes);
        if cur_node == end : return cur_time;      
        if isVisit[state][cur_node] == True: continue;
        else: isVisit[state][cur_node] = True;
            
        for next_node, next_cost, road_type in graph[cur_node]:
            next_state = state
            cur_isTrap = 1 if cur_node in trap_dict else 0;
            next_isTrap = 1 if next_node in trap_dict else 0;

            if cur_isTrap == 0 and next_isTrap == 0:
                if road_type == 1: continue
            elif (cur_isTrap + next_isTrap) == 1:
                node_i = cur_node if cur_isTrap == 1 else next_node
                isTrapOn = (state & (1<<trap_dict[node_i]))>>trap_dict[node_i]
                if isTrapOn != road_type: continue
            else:
                isTrapOn = (state & (1<<trap_dict[cur_node]))>>trap_dict[cur_node]
                n_isTrapOn = (state & (1<<trap_dict[next_node]))>>trap_dict[next_node]
                if (isTrapOn ^ n_isTrapOn) != road_type: continue
            
            if next_isTrap == 1:
                next_state = state ^ (1<<trap_dict[next_node])

            h.heappush(nodes,(cur_time+next_cost, next_node, next_state))

설명

---

🗣 Trash talk

상반기 카카오 인턴 코딩테스트에서 출제된 문제인데, 당시 5번과 더불어 나의 숨을 조여온 기억이 난다. 시험때 4, 5번을 건들지도 못했는데도 테스트에 통과했을 정도니 당시 시험을 본 사람 대부분이 나처럼 체감 난이도가 상당했을 것이다. 해당 문제의 해설은 이곳 에서 친절하게 알려주고 있다. 물론 풀이 코드는 제외하고 말이다.

📌 풀이 전략 요약

1. dijkstra 알고리즘을 이용하여 두 점 사이 경로를 찾는다.
2. bit mask를 이용하여 함정 노드들의 발동 상태(ON / OFF)를 구분 한다.
3. 방문 확인을 위한 isVisit 배열은 (함정 상태 경우의 수) x (전체 노드의 길이) 만큼의 길이를 갖는다.
4. 이를 이용해 이미 지나온 노드도 다른 상태(전체 함정들의 발동 상태)라면 재방문이 가능하다.
5. heapq를 사용해 최단 거리 경로들부터 확인한다. 따라서 end에 도달하는 순간이 정답이 된다.
6. heapq에는 직전 노드의 상태 정보를 넘긴다. 이 때문에 현재 상태를 따로 저장하고 갱신할 필요가 없다.

🎲 풀이 설명 (Python 기준)

1. 초기화

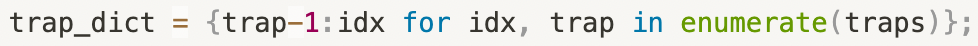
trap_dict에는 함정들의 정보가 담긴다.

• key에는 함정인 노드의 번호를 할당한다.
• value에는 각 함정의 순서를 할당한다.
  • 이는 비트마스크에서 각 함정을 뜻하는 자릿수로 사용된다.

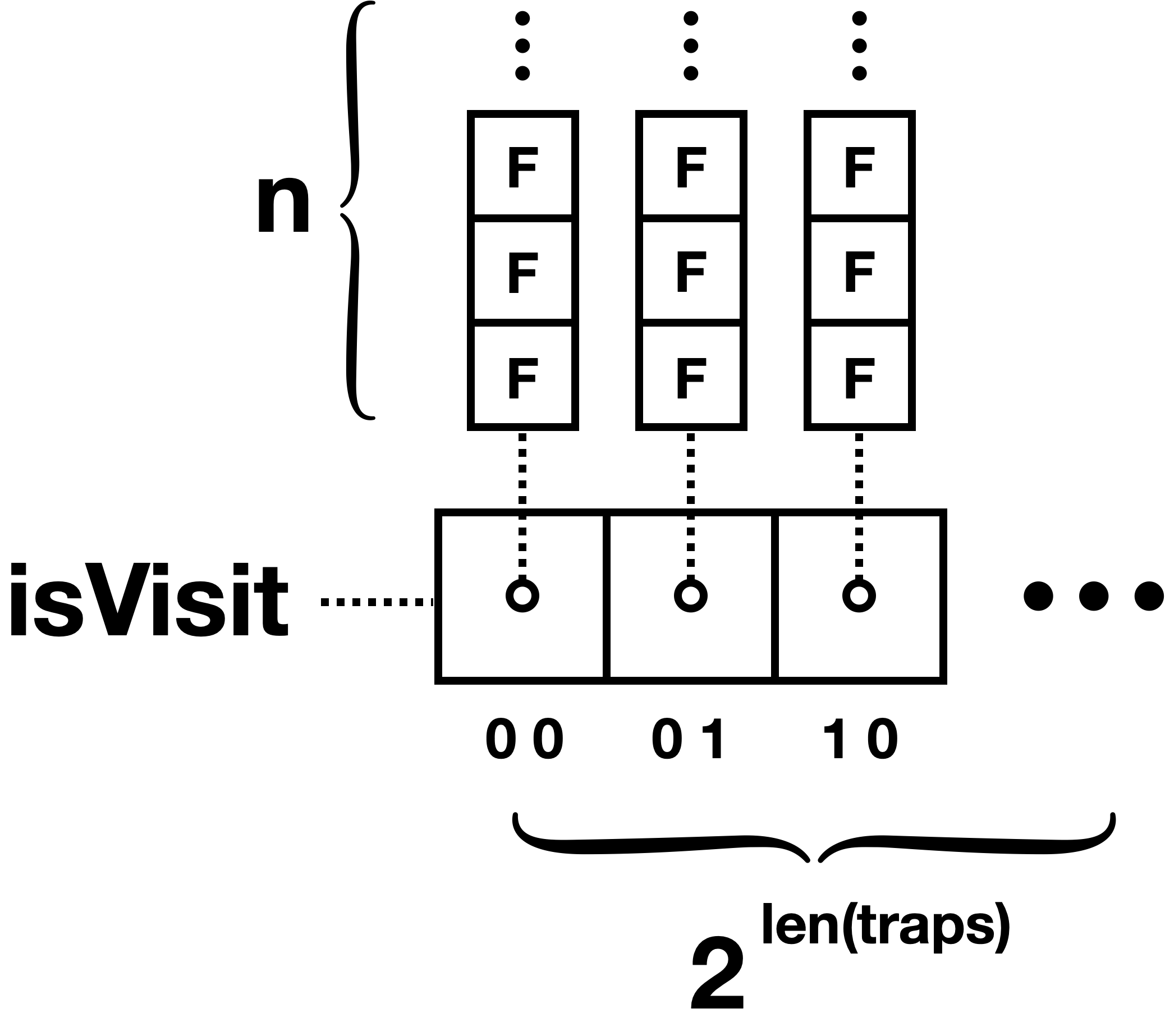
isVisit은 dijkstra의 방문노드 구분을 위한 2차원 배열이다.

• 첫 인덱스는 함정들의 고유 순서(자릿수)를 뜻한다.
• 두 번째 인덱스는 node번호를 뜻한다.
• 문제의 제한사항대로 함정 노드는 최대 10개다.
• 따라서 최대 $2^{10} = 1024$개의 함정 상태를 구분하면 된다.
• 함정 노드들의 상태 구분은 문제에서 주어진 traps의 길이를 시프트 연산하여 할당한다(첫 인덱스).

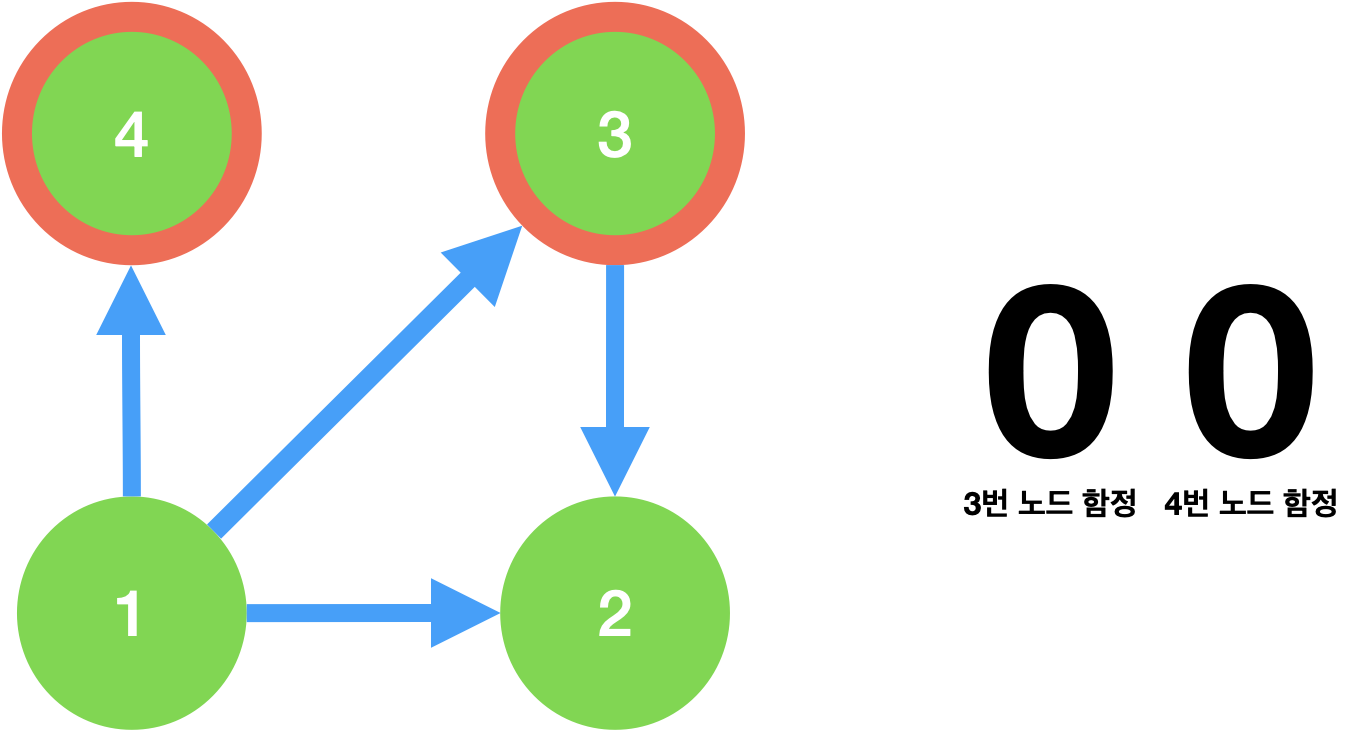
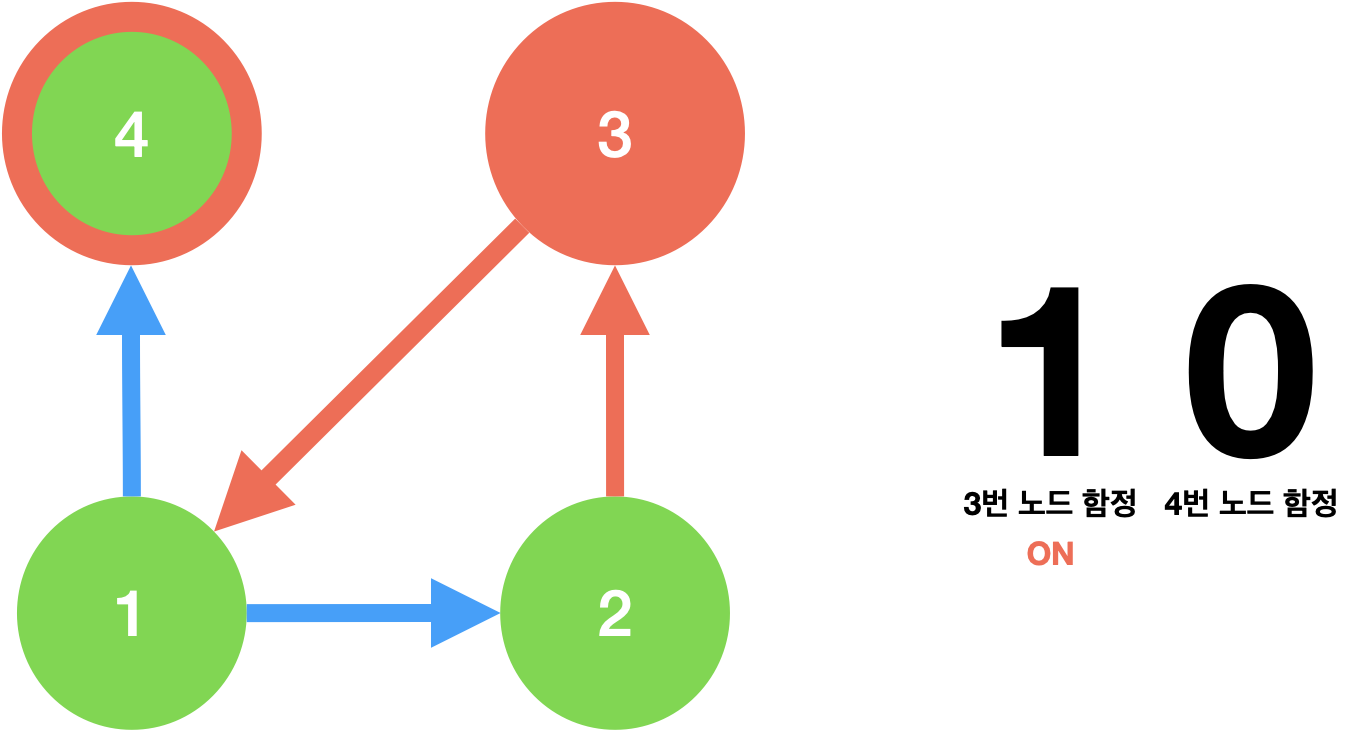
함정 상태의 0은 OFF, 1은 ON 상태를 뜻한다.

만약 위처럼 함정 노드(빨간 테두리 노드)가 2개인 그래프라면, 구분해야할 함정의 길이는 $2^2 = 4$이므로 4의 길이를 할당하면 되고 이는 [00, 01, 10, 11]의 상태를 뜻한다.

2. 간선정보 할당

• 간선들의 정보를 할당한다. 이때 정방향과 역방향을 구분하여 넣어준다.
• append로 할당되는 배열은 [목적지 노드번호, 이동비용, 다리의 방향 ] 이다.
• start 노드에게는 정방향(0)인 다리를, end 노드에게는 역방향(1)인 다리를 각각 할당한다.

3. heapq의 사용

heapq에는 다음과 같은 3가지 정보를 담은 튜플이 담긴다.

next_time: 해당 간선 이동시의 총 비용
next_node: 간선 이동시 도착 노드
next_state: 간선 이동 후 다음 노드 도착시 함정들의 상태

Python의 heapq 라이브러리는 튜플의 첫 번째 값으로 우선순위를 할당한다. 따라서 총 이동 비용이 최소인 간선들부터 순차적으로 확인할 수 있고, 만약 end 노드에 도착하면 현재 비용이 정답이 된다.

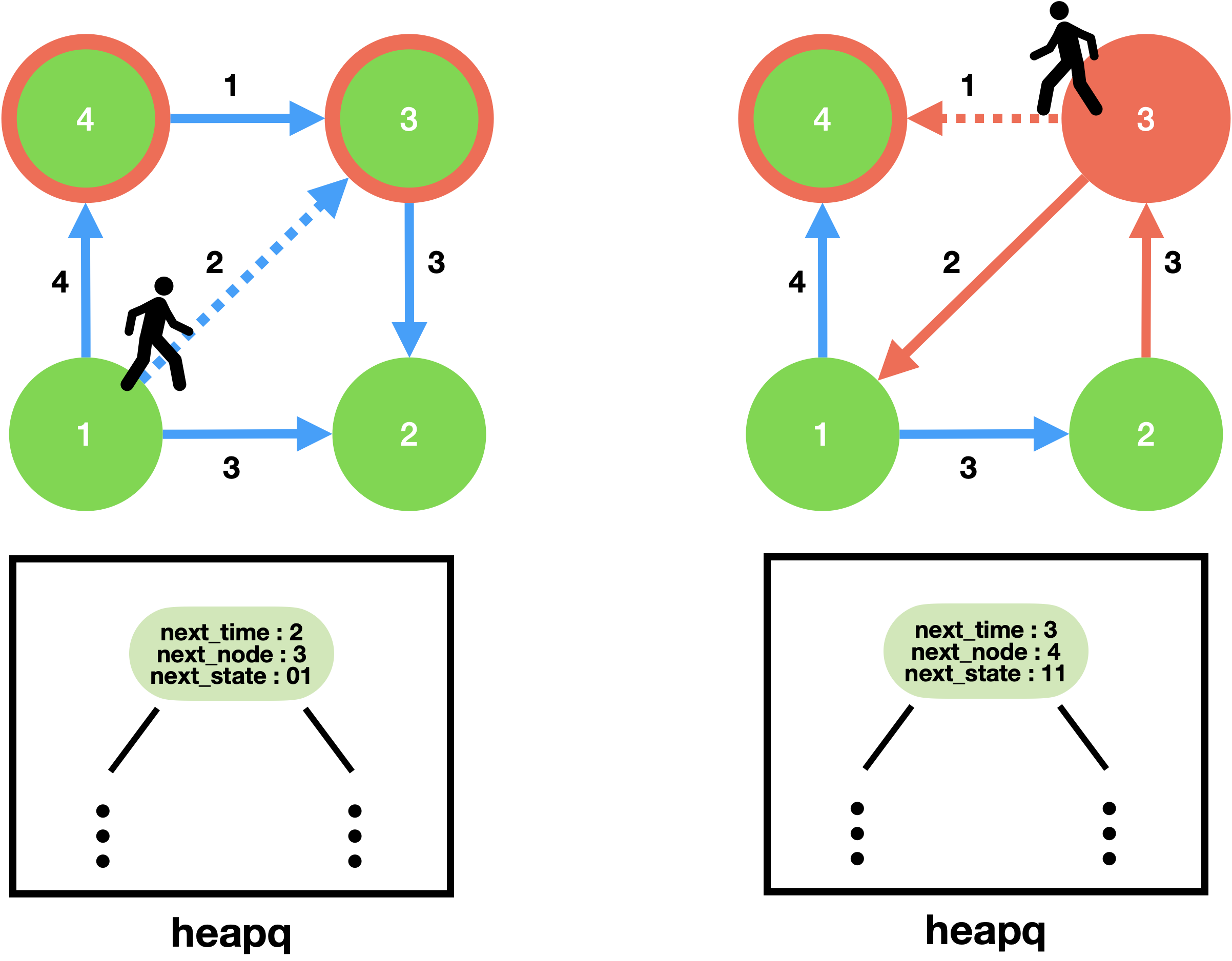
위 예시에서 놓쳐서 안되는 사실은, heapq에는 아직 1번노드 -> 2번노드 경로와 1번노드 -> 4번노드 경로가 남아있다는 것이다. 마찬가지로 오른쪽 이동을 통해 3번노드 -> 1번노드의 경로도 담기게 된다. 따라서 오른쪽 그림의 4번노드로 이동이 끝난 후 다음으로 pop되는 경로는 왼쪽 그림의 1번노드 -> 2번노드가 된다.

4. 현재 노드 검사

이제 시작 노드를 heapq에 넣고 반복문을 시작한다.

• heappop으로 heapq의 root를 가져온다.
  • cur_time, cur_node, state 정보를 변수에 할당한다.
• 현재 pop을 통해 가져온 정보는 이론상 최소거리의 간선과 도착 노드다.
• 만약 현재 도착 노드가 end면 현재 거리 비용을 리턴한다.
• 현재 노드의 상태(함정 state)를 확인하여 이미 방문한 노드라면 continue 한다.

아래 그림은 각 노드 방문시 isVisit 변수의 변화를 타나내는 예시다.

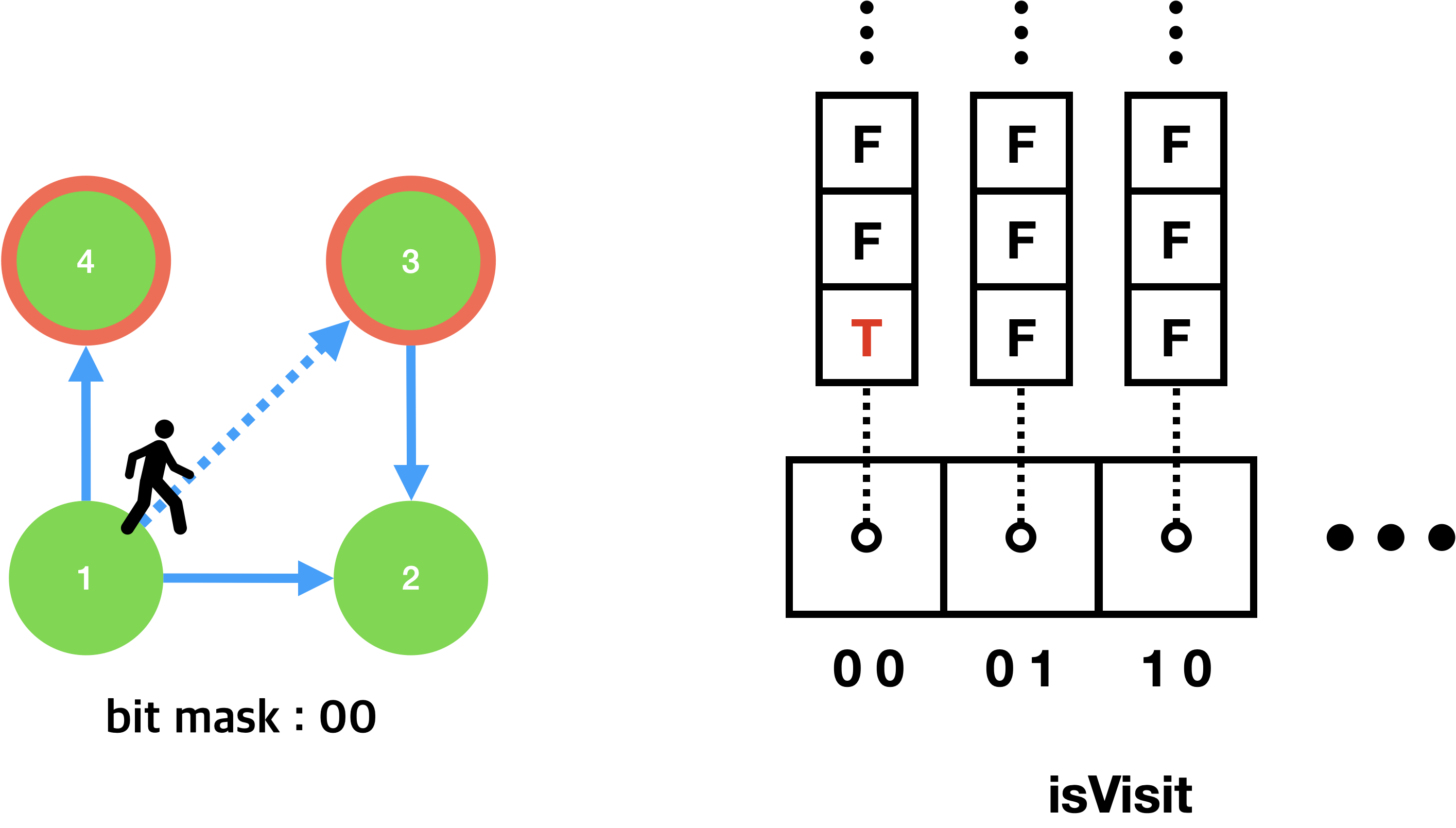
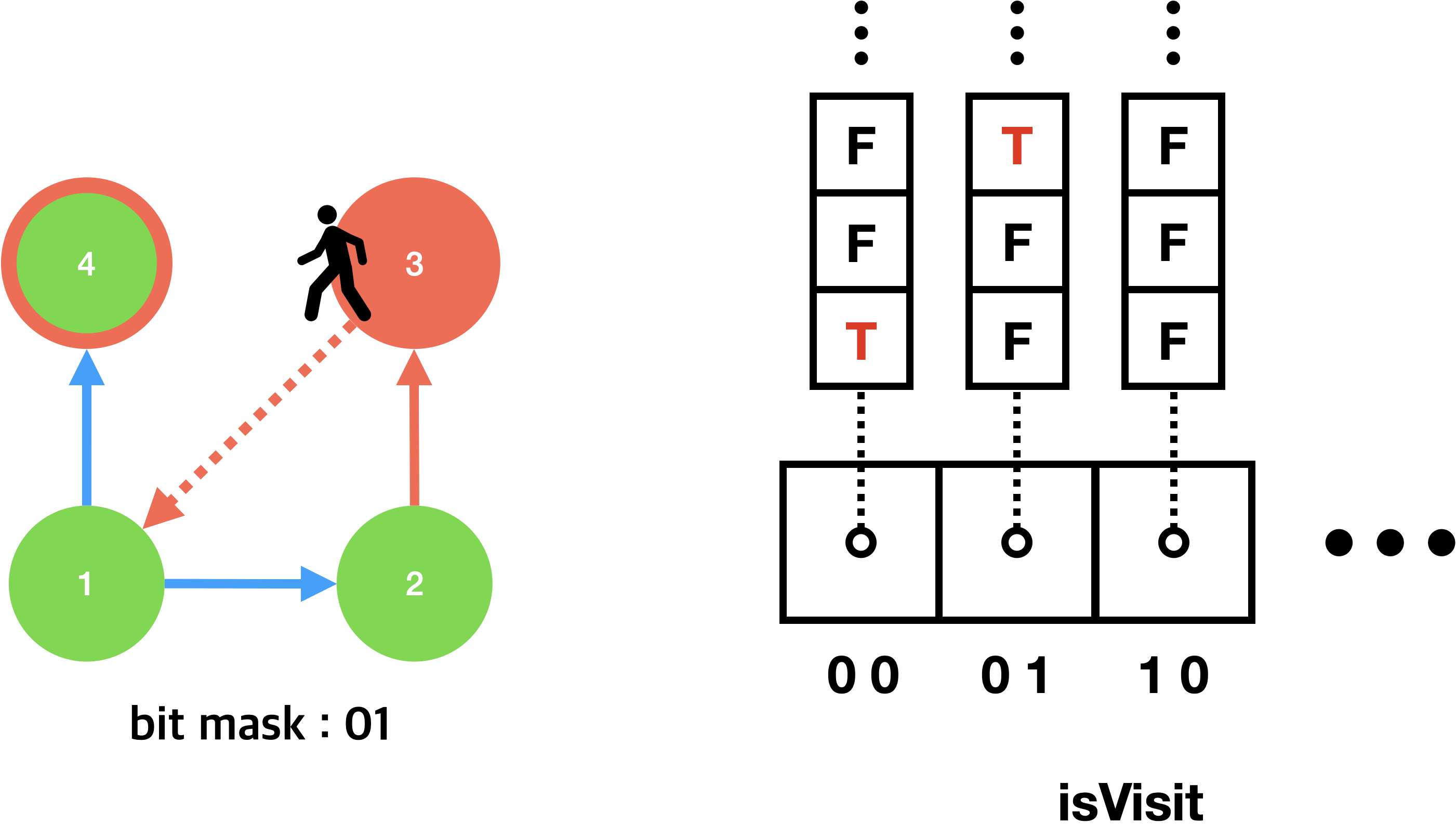
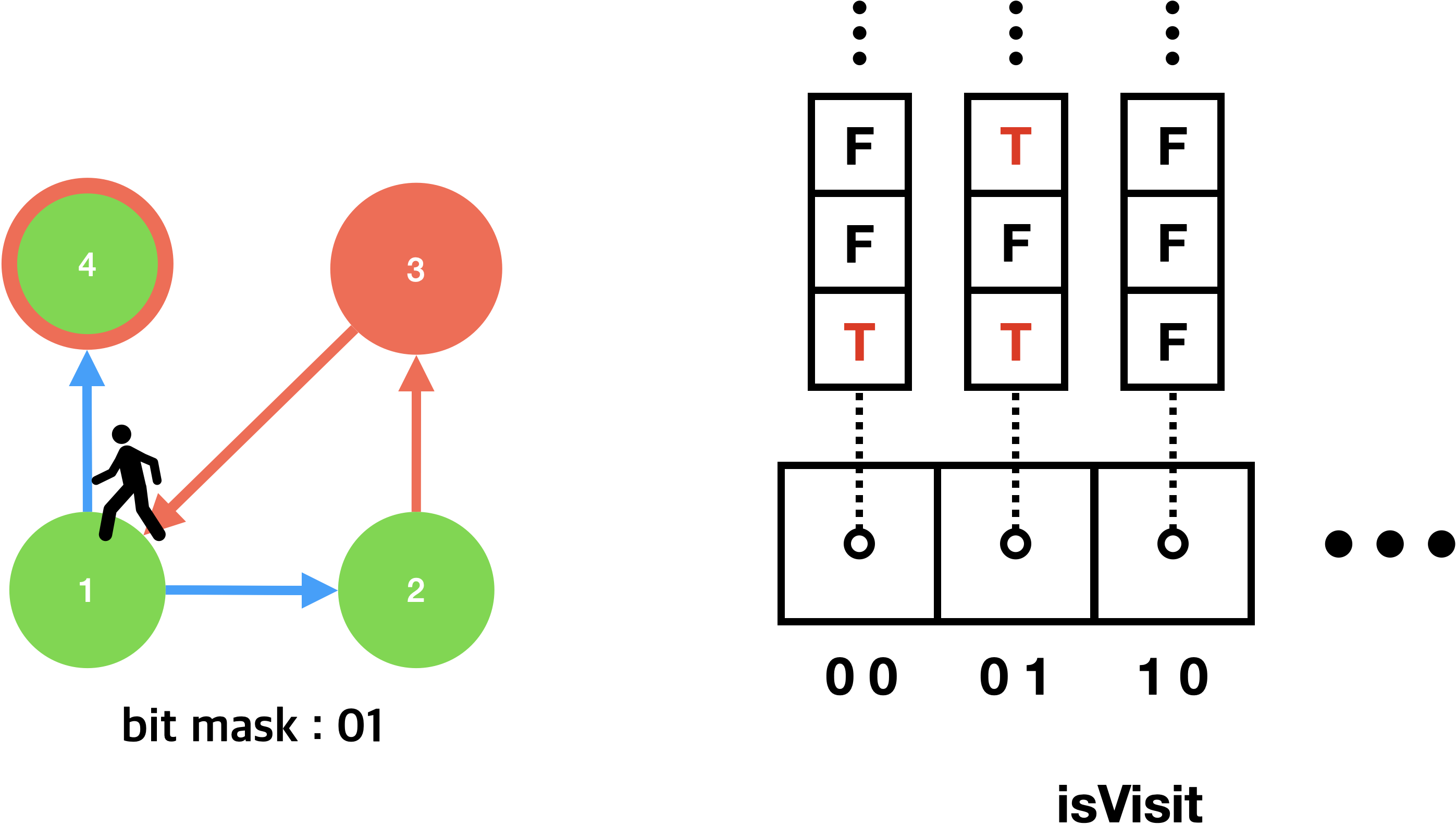
첫 그림과 마지막 그림에서 둘 다 1번 노드에 방문했지만, 이동할 때마다 state(bit mask)가 달랐기 때문에 isVisit에 할당된 값의 위치도 다르게 구별된다. 따라서 완전히 다른 노드에 방문한 것과 다르지 않다. 이런 메커니즘으로 함정의 발동 여부에 따라 재방문이 필요한 노드를 중복 없이 구별할 수 있다.

현재 노드의 검사 단계에서 문제가 없으면 다음 간선과 도착 노드에 대한 검증을 시작한다.

5. 검증

graph에서 현재 노드와 연결된 모든 간선을 불러와 다음과 같은 검증을 수행한다.

• 현재 노드와 다음 노드의 종류(함정 여부) 파악
• 현재 상태(state) 파악
• 다음 간선의 종류(방향) 파악
• 이동후의 상태(next_state) 파악

이는 현재 주어진 간선으로 다음 노드로의 이동이 가능한지, 가능하다면 이동 후 상태가 어떻게 바뀔지 알기 위해서 수행하는 작업들이다.

현재 노드의 종류(일반, 함정)와 다음 노드의 종류(일반, 함정)에 따라 크게 4가지 경우의 수가 생긴다.

1. 일반노드 -> 함정노드
2. 함정노드 -> 함정노드
3. 함정노드 -> 일반노드
4. 일반노드 -> 일반노드

각 종류의 이동 패턴은 다음 그림과 같다.

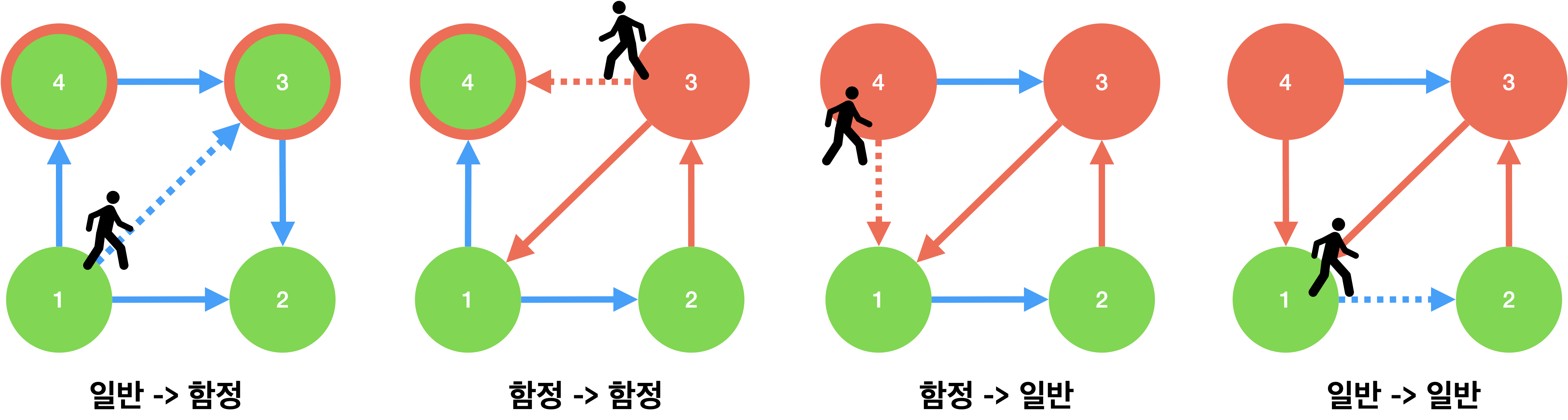
이를 통해 다음과 같은 사실들을 알 수 있다.

• 일반->일반 이동이 가능하려면 간선이 반드시 정방향이어야 한다.
• 일반->함정 혹은 함정->일반 이동시 다음 두 가지 상황에서 이동이 가능하다.
  • 함정이 발동한 상태에서 역방향 간선
  • 함정이 발동하지 않은 상태에서 정방향 간선
• 함정->함정 노드 이동시 다음 세 가지 상황에서 이동이 가능하다.
  • 두 함정 모두 발동되지 않은 상태에서 정방향 간선
  • 두 함정 모두 발동된 상태에서 정방향 간선
  • 한 함정만 발동된 상태에서 역방향 간선

이는 다음과 같은 코드로 표현된다.

isTrapOn은 현재의 상태(state)에 특정 함정의 시프트 연산(<<)과 end(&) 연산을 통해 특정 함정이 작동되어 있는지를 나타낸다. 이를 통해 현재 불러온 간선을 통해 이동이 가능한지 판단할 수 있다.

6. heappush

여기까지 모두 통과하여 도착한다면 이는 다음과 같이 요약할 수 있다.

[heapq에서 꺼내온 최단거리 경로 노드]에서 [해당 노드와 연결된 모든 간선 중에 현재 선택된 간선]으로 이동이 가능하다.

이제 마지막으로 이동이 가능한 경로를 다시 heapq에 넣으면 된다.

앞에서 heapq에 담겼던 내용은 next_time, next_node, next_state였다.

이제 이 세가지를 현재 선택된 간선을 기준으로 계산하면 된다.

next_time: 현재 이동 비용 + 간선 이동 비용
next_node: 간선 이동시 도착 노드
next_state: 간선 이동 후 다음 노드 도착시 함정들의 상태

다음 방문할 노드가 함정이 아니라면 현재 state를 넘긴다.

만약 다음 방문할 노드가 함정이라면, 다음 노드의 함정이 작동된 상태를 시프트연산을 통해 갱신하여 넘겨줘야 한다.

이로써 heappush의 과정마저 끝났고, end에 도착할때까지 위 과정을 반복하면 된다.

🔴 질문이나 개선이 필요한 부분 등 적극적인 피드백 환영! 🔴